TOP 自分の思い 邪馬台国 バイク 瓢箪 霊場巡り 囲碁と将棋 CAD/CAM 生産管理 海外の思い出 索引
金型でのCAE試行錯誤事例
・3次元測定機とのリンク
金型というのは精度のあやふやな世界だと思う
金型自体は最低でも1/100mmの精度でないといけない
最も公差が厳しいのは嵌め合いのある部品である
例えばエジェクタピンとピンを通す穴とは隙間が3〜5/1000mm
位の誤差でないときつすぎるか、ゆるすぎるかしてしまう
板と板の隙間も同様である
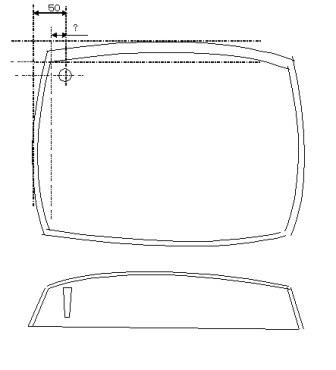
しかし、出来上がった製品を見ると、バリはあるは、平面の
はずが曲面になってしまうはで、人間の目で見ても寸法が
変なのが判る位、誤差が出る
お客とのもめ事も出来上がった品物を見てから勃発するの
が常である
だから、工場では品質責任者というのを置いていた
品質部門には3次元測定器という品物の寸法を測り、デー
タで記憶する装置が置いてあった
台座が温度による誤差が少ない石で出来ており、表示板に
は小数点以下3桁(1/1000)の数字が表示されていた
これで金型を出荷するまえに試し打ちした製品を測定し、条
件を添付して、温度、湿度、金型動作条件がそろえば、この
位の誤差のある製品が出来ますと言う保証書を付けて納品
するのである
その他に、こんなもの使えるかといってお客が品物を持ち
こんできたものを実際どの位変形しているか調べたりして
いた
このどの位変形しているかを自動的に出せないかというのが
私に持ち込まれた課題である
そこで、例によって3次元測定器からデータを貰い、CADで
読ませる所から調査を始めた
想定した手順は
・3次元測定機で実物を測定、X,Y,Zの測定点群データ作成
・CADマシンでASCII文字列に変換
・IGES言語にする
・CADで図形に変換(点群にする)
・製品形状をCADに表示する
・点群をCAD形状に投影し、製品までの距離を出す
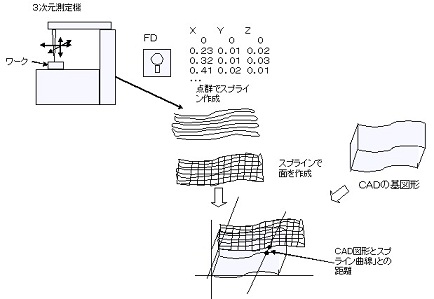
やってみたら、点が一杯でわけがわからない
3次元測定器は自動的に測定できるので、0.1mm刻みで
1000個位測定するのはわけがない
しかも、各々の点と、製品形状の線とが比較しようがない
測定するのは製品の端ではないのである
そこへ勾配の問題が絡むので更にややこしい
(CAD機能強化2の項で説明したが、図面表記するのは、仮想点
の寸法である、実際に測れるのは丸まった角で図面には示せない)
そこでIGES変換でなくCAD図形言語に変換し、スプライン
曲線を発生させることにした
これは点群をXn、Ynとしたとき、始点X1、Y1から距離が近
い順に並べていき、スプライン曲線のコマンドの要素として、
点群を変換して繋げていくプログラムを作るという意味である
折り返しをどうするか難しかったが、なんとか解決し、面を貼る
ことに成功した
これと最初にCADで作った形状とをどの場所で比較するかを
指定し、CADから上下方向に線分を発生させて、スプライン
曲線との交点を求め、CAD面との距離を求めて一覧表を作成
する
結果がどう使われたのかは確認していない
推測するにお客へは出せないと思った
寸法に対して1/100程度の誤差なら良いが、2〜3mm違うの
である
特に製品がねじ曲がる方向に変形した場合は大きな誤差が出た
この手法は3次元測定器のメーカーが欲しがったが、CADシス
テムでないと動作しないため、諦めたようであった
私はこれを実用新案にするつもりはなかったが、他社で先に
実用新案を取られると自分で作ったものが自分で使えない事
態になる
CAD業界の発展に寄与するというと大げさだが、みんなに手法を
PRし、やれば出来るよと鼓舞したかった
その意味では特許とか実用新案というのはけつの穴の小さい輩
のつまらない所業に思えてならない
あれから30年、もし未だにこの程度の事が実現できていないなら
実用新案なんか関係ない、やれるものなら猿まねでも何でもやっ
てみろといいたい
事のついでに肝となる部分の「近傍」について説明しておく
案外この方が知的所有権に引っかかるかも
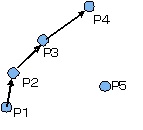
右図のP3からP5でなくP4へ線分をつなぎたいとする
人間ならP2,P3と来たのだからP4に決まっているよと判断する
CADで同じことを判断するには、どちらが近いかと、方向はどちら
があっているかの両方から判断する
2点間の距離は(x3−x4)^2+(y3−y4)^2 と(x3−x5)^2+
(y3−y5)^2の小さい方が近い
方向は(x2−x3)/(y2−y3)−(x3−x4)/(y3−y4)と
(x2−x3)/(y2−y3)−(x3−x5)/(y3−y5)の絶対値の小さ
い方がより方向があっている
だからP4を選ぶとしていく、簡単な中学校で学んだ程度の数学で
あるが、いざ思い出すとなると難しいようなので掲載した
次へ


