TOP 自分の思い 邪馬台国 バイク 瓢箪 霊場巡り 囲碁と将棋 CAD/CAM 生産管理 海外の思い出 索引
磁
場理論展開
ー天石流における磁場の詳細解説ー
1 磁場の定義
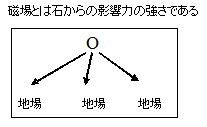
石は盤面に置かれた時点で単体で回りに影響を与えている
この影響力を磁場と名づける、地になる確立と解釈しても良い(図1)
図1
影響力には2種類ある
地を作ろうとする力を囲碁用語で地模様という
地にし易くする力を模様あるいは勢力という
相手の石に対しては反対の力として作用する
地を作らせないようにする力
地にしづらくする力
磁場の複合
2つの石を結んだ直線を磁場線と名づける(図2)
味方どうしの石と石の間は2つの石の磁場が合計される
磁場線上の磁場が最も強力でありその周囲も距離に応じた磁場になる
3方から箱型に磁場線に囲まれたエリアを模様という
図2

2 磁場の強さ
図3

磁場の強さは石の距離に反比例する
距離は縦横方向に線の本数で数える
斜め方向は線の数であるから縦横の2倍になる
それぞれの石が1つでなく複数の場合は石数に応じて磁場が強くなる
石数に応じてとは石の直径の大きさという意味である(後述)
3 辺の扱い
盤面の端はそこから先の磁場がゼロになるラインとする
4 相手の石との関係
相手の石とは打ち消しあうように磁場が働く
5 石の大きさ
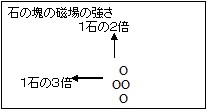
複数の石が密集している場合一つの大きな石と見てその直径を
石の大きさと考える(図4)
図4

例えば4つの石がいわゆる団子状になっている場合、その直径は
縦からも横からも2倍の大きさと見ることが出来る
縦に4つ並んでいる場合は垂直方向からは直径は4倍だが
水平方向からは直径は1である
6 石の大きさの密度による変化
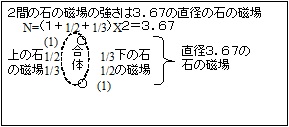
例えば4つの石が2間の幅で4角に並んでいる時は、直径は4である
しかし密集して4つづつ並んだ石と大きさを同じとして良いのか
ここで石の集団の磁場発生方向から見た密度の合計と完全密集の
場合の合計の比率を掛けることとする
上記4つの石の場合は両端は1であるが中央の2ヶ所は5/6である
合計は3と2/3になり、密集の場合の4に比べ若干弱くなる
つまり2間に並んだ2つの石の磁場線から発する磁場は3.67を石の直径とする
磁場とみなすこととする
7 磁場の地獲得の限界値
図5
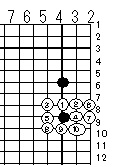
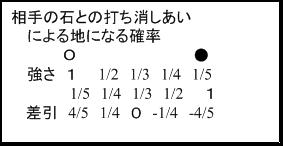
経験値から2つの石の間が地になるのは2間、3線、あるいは2立3斥
といわれてきたが、今まで述べた磁場の理論で数値化してみる
例えば3線に2間に開いた石は約10目の地をほぼ確定したと言われるが
具体的に図の①~⑦の地になる確率を計算してみると
①=1/2+1/3=5/6
②=1/3+1/4=7/12
③= 同 =7/12
④=1/2+1/5=7/10
⑤= 同 =7/10
⑥=1/4+1/5=9/20
⑦=1/3+1/6=1/2
⑧=1/3+1/6=1/2
⑩= 同 =1/2
⑨=1/2+1/5 (2石が重なっており陰になった石の影響は1/5よりも小さいと考えられる)
ただし③~⑩はこの図以外に石があった場合その石の影響も受ける
仮に①から⑩までの数値を足してみると、7.2となる
この2倍の14目強に磁場の計算式の定数1/4を掛けた約3~4目
が確定地と一般的には考えられる
つまり2つの石の磁場の総和が1/2以上の地点は地になると考えられる
では次図はどうか、
図6
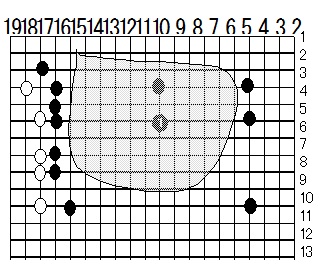
図の灰色に塗りつぶした辺りの地はどのくらいの割合で地といえるのか
感覚的には①を打った時点で確定地といえるのではないか
少なくとも5線辺りまでは確定、6線以上は5~7割確定といった感じと思う
②の場所、③の場所、5の場所を計算すると
左辺
②=1/6+1/4+1/5+1/6+1/8+1/9+1/10
中央
+1/5+1/7
右辺
+1/11+1/13+1/18
白石は背後にくっついているため計算から除外した
=約1.5X定数1/4=0.4
③=1/10+1/8+1/7+1/6+1/4+1/5+1/6
+1/9+1/7+1/15+1/13+1/14
=約1.3X定数1/4=0.3
⑤=1/3+1/6+1/7+1/9+1/10+1/11+1/13+1/10
+1/12+1/11+1/16+1/18
=約1.3X定数1/4=0.3
先ほどの2間開きでは1/2以上の確率で地と判断したが
同じように計算すると②も③も確定地となる、⑤も確定地であり
少し感覚と狂ってくる
これは中央の不確定差が経験値では大きく反映するからと思われる
前図の③⑤⑨とこの図の⑤の地点は感覚的には半分くらいであろうか
例えば⑤の地点は6割の確立で地になるといわれたら模様が好きな
人なら賛成するであろう
以上の経験値との比較から
①磁場の総和が0.2以上の場所はほぼ確定地である
②ただし、中央に開けた場所では確立は1/2になる
天石流の磁場説明に戻る 天石流TOP TOP








